反射容斥小记

, ,

〇、前言

两个星期模拟赛出现了两次。正好两次都没做出来。

ZJ 说这个套路已经要烂了。可是我才刚入门啊/kk。

不过这东西本身很简单，关键在于是否能推出一个 dp，然后找到 dp 的组合意义是这样再优化。

一、思想讲解

这东西我都不愿意称之为算法。

考虑一个二维平面，只能向右边或者上面走。从 $(0,0)$ 走到 $(n,m)$ 的方案数是 $\dbinom{n+m}{n}$。

而假设我们现在有一条线 $y=x+b$ 不可以碰撞。

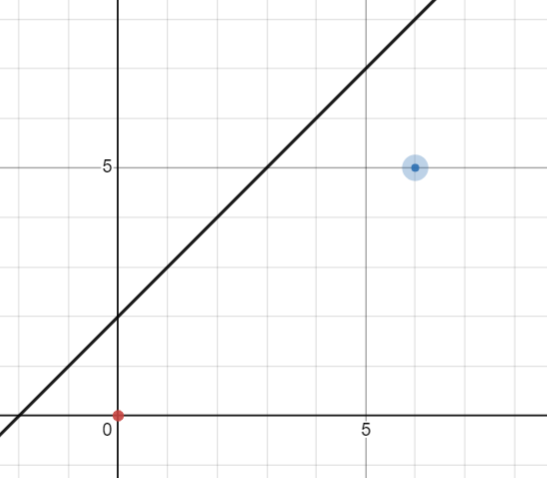
对于碰撞到这条线的路径，从碰撞第一次开始反转，结束位置变成 $T(n,m)$ 关于 $y=x+b$ 对称的点 $T’(m-b,n+b)$（这是点在直线右下角的情况，再左上方同理）。

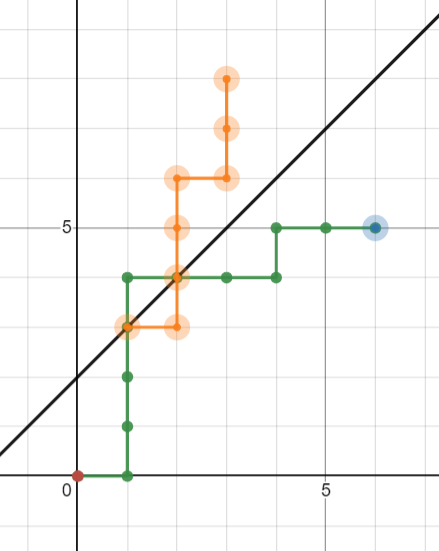
容易发现一条走到 $T’$ 的路径翻折之后都是一条经过了 $y=x+b$ 的路线。（这里指的是如果碰到线上一个点也算）。

因此答案为 $\dbinom{n+m}{m}-\dbinom{n+m}{m-b}$。

如果有两条的情况，设第一条直线为 $A$，碰到第二条直线的为 $B$。记 $AB$ 表示碰到 $A$ 再碰到 $B$ 的路径。采用容斥的思想，什么都没碰到 $-$ 先碰到 $A$ 的路径 $-$ 先碰到 $B$ 的路径 $+$ 先碰到 $AB$ 的路径 $\dots$。

反射多次的怎么求呢？设终点经过 $A$ 反射之后的点为 $T_A$，则经过 $AB$ 反射之后的点为 $T_{AB}$。碰到 $AB$ 的路径则与起点到 $T_{AB}$ 的一一对应。

如果什么时候对应到 $x<0$ 或者 $y<0$ 了，就停止。

二、例题

2.1 头文字 O

Description

有一个数轴。车初始在原点。每时刻随机位置向左 $-1$，或向右 $+1$。有 $m$ 条规则，第 $i$ 个规则形如 $(s_i,t_i,v_i)$ 表示存在经过 $s_i$ 后经过 $t_i$ 则获得 $v_i$ 的价值。求 $n$ 时刻后期望获得的价值。

$n\le 2\times 10^5,m\le 5\times 10^5,-n\le s_i,t_i\le n$。

有部分分：$0\le s_i\le t_i\le n$。

Solution

根据期望的线性性这 $m$ 个规则是独立的，可以独立计算。

先考虑部分分。部分分去掉了 $s_i$ 的限制，也就是走到 $t_i$ 即可。考虑用总共的减去走不到 $t_i$ 的，观察发现就是给定一个二维网格，不经过 $y=t_i$ 这条直线的方案数。这样可以套用一条直线的反射容斥计算。

部分分会做了，考虑正解。不妨假设 $s_i\le 0\le t_i$ 的情况，其实是和 $(s_i,2s_i-t_i)$ 的情况是一样的，也就是把 $t_i$ 对称过去就不用考虑 $s_i$ 了。就转化成了部分分的情况。

复杂度 $O(n+m)$。

2.2 [JLOI2015] 骗我呢

令 $f_{i,j}$ 表示考虑到第 $i$ 行，第 $i$ 行不选的是 $j$。则有转移：$f_{i,j}=\sum_{k\le j+1}f_{i-1,k}$。

考虑组合意义，即求下图从起点走到终点的方案数：

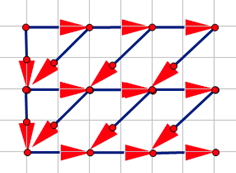
iwUEt0.png

考虑变形一下就是：

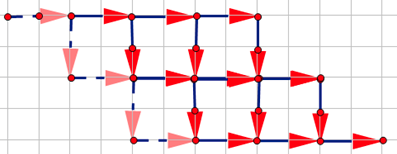
iwUwBd.png

即不经过两条直线：

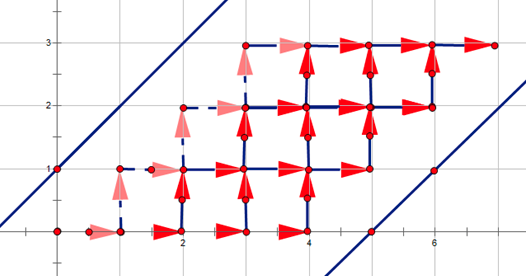
iwUt1O.png

的方案数。

形式化的说，求从 $(0,0)$ 走到 $(n+m+1,n)$ 的路径条数满足不经过 $y=x+1$ 和 $y=x-(m+2)$。

然后套用反射容斥即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
int N=3e6+2;
int n,m,suf[maxn],isuf[maxn],ans;
void add(int &x,int y) {x=(x+y)%mod;}
int C(int x,int y) {return x<0||y<0||x<y?0:suf[x]*isuf[x-y]%mod*isuf[y]%mod;}
signed main(void){
	int i,j,x,y;
	read(n);read(m);
	for (suf[0]=1,i=1;i<=N;i++) suf[i]=suf[i-1]*i%mod;
	for (isuf[N]=power(suf[N]),i=N;i>=1;i--) isuf[i-1]=isuf[i]*i%mod;
	x=m+n+1,y=n;
	ans=C(x+y,x);
	for (i=1;i<=n;i++) {
		if (x<0||y<0) break;
		if (i&1) {
			int p=abs(x-(m+2)-y);
			x+=p,y-=p;
			add(ans,mod-C(x+y,x));
		}
		else {
			int p=abs(x+1-y);
			x-=p,y+=p;
			add(ans,C(x+y,x));
		}
	}
	x=m+n+1,y=n;
	for (i=1;i<=n;i++) {
		if (x<0||y<0) break;
		if (i&1) {
			int p=abs(x+1-y);
			x-=p,y+=p;
			add(ans,mod-C(x+y,x));
		}
		else {
			int p=abs(x-(m+2)-y);
			x+=p,y-=p;
			add(ans,C(x+y,x));
		}
	}
	printf("%lld\n",ans);
	return 0;
}

2.3 一般难度的推式子题

考虑暴力。令 $f_{i,j}$ 表示子树大小为 $i$，高度 $\le j$ 的方案数。

正解其实和 dp 没有太大关系。考虑一个严格弱的问题，树大小为 $x$ 的方案为多少。推一推发现是卡特兰数。

所以考虑组合意义求 $f_{i,j}$。回顾卡特兰数的推导，用欧拉序的出栈入栈理解，起点 $(0,0)$，终点 $(n-1,n-1)$，入栈 $y+1$，出栈 $x+1$，不能触碰 $y=x-1$ 的方案数。

加上 $j$ 的限制，也就是又加了一条直线 $y=x+(j+1)$ 不能碰。用经典的反射容斥做。$j$ 的反射次数是 $O(\dfrac{n}{j})$，最后复杂度是 $O(n\ln n)$ 的。

图片都是贺的。