Description
https://www.luogu.com.cn/problem/P3473
Solution
还是一些细节没想清楚啊。
观察到每次相当于切割一次矩阵,我们令 $f_{i,j,k,l,0/1/2/3}$ 表示矩阵的左下角的为 $(i,j)$,右上角为 $(k,l)$,接下来要往 上/右/下/左 走。
先不考虑有障碍的情况。
感觉从 $(1,1)$ 开始不好赋初值啊,于是我们考虑从 $(sx,sy)$ 开始倒着走,也就是每次左转。比如我们以往上走为例子:
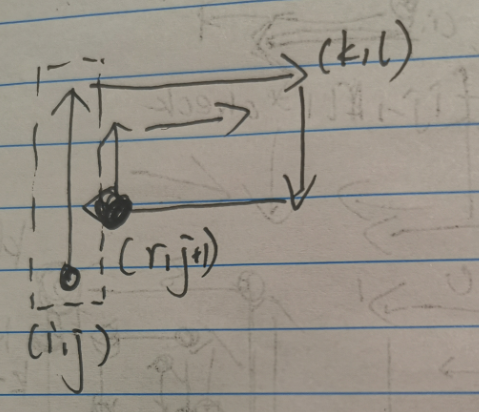
$f_{i,j,k,l,0}\gets f_{r,j+1,k,l,1}$。
考虑用已经递推出来的来化简这个东西:
$f_{i,j,k,l,0}\gets f_{i+1,j,k,l,0}+f_{i,j+1,k,l,1}$。
可以发现新加入的一条是列为 $j$,行 $[i,k]$ 的一列值,只需要判断这一段上没有障碍就可以转移。
同样的可以扩展到剩下 $3$ 种情况。
最初状态 $f_{sx,sy,sx,sy,i}=1$。
然后考虑转移方向,观察到每次让矩形的半周长增加 $1$。所以我们先枚举矩形半周长即可。
这样就可以 $O(n^4)$ 递推了。空间需要滚动数组优化,复杂度为 $O(n^3)$,有 $8$ 倍的常数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define maxn 105
#define put() putchar('\n')
#define Tp template<typename T>
#define Ts template<typename T,typename... Ar>
using namespace std;
Tp void read(T &x){
int f=1;x=0;char c=getchar();
while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
while (c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
x*=f;
}
namespace Debug{
Tp void _debug(char* f,T t){cerr<<f<<'='<<t<<endl;}
Ts void _debug(char* f,T x,Ar... y){while(*f!=',') cerr<<*f++;cerr<<'='<<x<<",";_debug(f+1,y...);}
#define gdb(...) _debug((char*)#__VA_ARGS__,__VA_ARGS__)
}using namespace Debug;
#define fi first
#define se second
#define mk make_pair
int n,m,mod;
int r[maxn][maxn],c[maxn][maxn],a[maxn][maxn];
int sx,sy,ans;
int f[2][maxn][maxn][maxn][4];
signed main(void){
int i,j,k,l,o,s,lenx,leny;char ch;
read(n);read(m);read(mod);
read(sy);read(sx);sx=n-sx+1;
for (i=n;i>=1;i--) {
cin>>ch;
for (j=1;j<=m;j++,ch=getchar()) a[i][j]=(ch=='*');
}
for (i=1;i<=n;i++) for (j=1;j<=m;j++) c[i][j]=c[i][j-1]+a[i][j],r[i][j]=r[i-1][j]+a[i][j];
for (s=2;s<=n+m;s++) {
int now=s&1,pre=now^1;
memset(f[now],0,sizeof(f[now]));
for (lenx=1;lenx<s;lenx++) {
leny=s-lenx;
for (i=1,k=lenx;i<=sx&&k<=n;i++,k++) {
for (j=1,l=leny;j<=sy&&l<=m;j++,l++) {
if (k<sx||l<sy) continue;
f[now][j][k][l][0]=(f[pre][j][k][l][0]+f[pre][j+1][k][l][1]+(i==sx&&j==sy&&k==sx&&l==sy))*(r[i-1][j]==r[k][j])%mod;
f[now][j][k][l][1]=(f[pre][j+1][k][l][1]+f[pre][j][k-1][l][2]+(i==sx&&j==sy&&k==sx&&l==sy))*(c[k][j-1]==c[k][l])%mod;
f[now][j][k][l][2]=(f[pre][j][k-1][l][2]+f[pre][j][k][l-1][3]+(i==sx&&j==sy&&k==sx&&l==sy))*(r[i-1][l]==r[k][l])%mod;
f[now][j][k][l][3]=(f[pre][j][k][l-1][3]+f[pre][j][k][l][0]+(i==sx&&j==sy&&k==sx&&l==sy))*(c[i][j-1]==c[i][l])%mod;
}
}
ans=(ans+f[now][1][lenx][leny][0])%mod;
}
}
printf("%d\n",ans);
return 0;
}
|
