HHHOJ胡策题3 数据库

,

Description

image-20231107153045425

$n,q\le 5\times 10^3,m\le 15$

1s 512MB

Solution

CF802C 加强版。

考虑网络流。

解法1

一种考虑正着直接做，使得不删除的费用最小。

观察到如果一个数要给下一个数用，令相邻的两个颜色相同的数的位置分别为 $i,j$，$i<j$，则 $i$ 必须要一直放到 $j$ 之前，等价于在 $j-1$ 以 $-w_{a_i}$ 的代价删去，而 $j$ 只能删一次（满足最大流），所以要新建一个点限制一下。

有建图：

这样点数 $2q$，边数 $5q$。其实不是很能过。

解法2

考虑正难则反，不用选的最大。

最开始限制流量 $m-1$。

新建 $q$ 个点，$(i,i+1)$ 赋 $(m-1,0)$。如果 $i,j,i<j$ 为颜色相同的两个相同的数，则连边 $(i,j-1,1,-w_{a_i})$ ，表示如果保留 $i$，则要占用这一段的点。

然后跑 EK 即可。点数 $q$，边数 $2q$，EK 可以稳过。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define maxn 20005
#define put() putchar('\n')
#define Tp template<typename T>
#define Ts template<typename T,typename... Ar>
using namespace std;
Tp void read(T &x){
    int f=1;x=0;char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
    while (c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
    x*=f;
}
namespace Debug{
	Tp void _debug(char* f,T t){cerr<<f<<'='<<t<<endl;}
	Ts void _debug(char* f,T x,Ar... y){while(*f!=',') cerr<<*f++;cerr<<'='<<x<<",";_debug(f+1,y...);}
	#define gdb(...) _debug((char*)#__VA_ARGS__,__VA_ARGS__)
}using namespace Debug;
#define fi first
#define se second
#define mk make_pair
const int mod=1e9+7;
int power(int x,int y=mod-2) {
	int sum=1;
	while (y) {
		if (y&1) sum=sum*x%mod;
		x=x*x%mod;y>>=1;
	}
	return sum;
}
int ans;
int n,m,w[maxn],a[maxn],q,nums[maxn],p[maxn];
const int inf=1e9;
int s,t;

namespace EK{
	int head=1,h[maxn];
	struct yyy{
		int to,z,w,val;
		inline void add(int x,int y,int a,int b){
			to=y;z=h[x];h[x]=head;w=a;val=b;
		}
	}a[1000005];
	inline void ins(int x,int y,int z,int val){
//		gdb(x,y,z,val);
		a[++head].add(x,y,z,val);
		a[++head].add(y,x,0,-val);
	}
    queue<int>q;
    int dis[maxn],pre[maxn],in[maxn],s,t;
    int ans,anss;
    inline bool bfs(void){
    	int i,x;
    	memset(dis,0x3f,sizeof(dis));
    	dis[s]=0;in[s]=inf;q.push(s);
    	while (!q.empty()){
    		x=q.front();q.pop();
    		for (i=h[x];i;i=a[i].z)
    		    if (a[i].w&&dis[a[i].to]>dis[x]+a[i].val) {
    		    	dis[a[i].to]=dis[x]+a[i].val;
    		    	in[a[i].to]=min(in[x],a[i].w);
    		    	pre[a[i].to]=i;q.push(a[i].to);
				}
		}
		return dis[t]<inf;
	}
	inline void add(void){
		int now=t;
		int x=in[t];
		while (now!=s) {
			a[pre[now]].w-=x;
			a[pre[now]^1].w+=x;
			now=a[pre[now]^1].to;
		} 
		ans+=in[t];anss+=in[t]*dis[t];
	}
	inline void EK(int x,int y){
		s=x;t=y;
		while (bfs()) add();
	}
}
using EK::ins;
namespace BL {
	void main(void) {
		int i;
		for (i=1;i<=n;i++) nums[a[i]]++,ans+=w[a[i]]*(nums[a[i]]==1);
		printf("%lld",ans);
	}
}
signed main(void){
//	freopen("1.in","r",stdin);
	int i,j,ans=0;
	read(n);read(m);read(q);
	for (i=1;i<=n;i++) read(w[i]);
	for (i=1;i<=q;i++) read(a[i]);
	s=0,t=q+1;
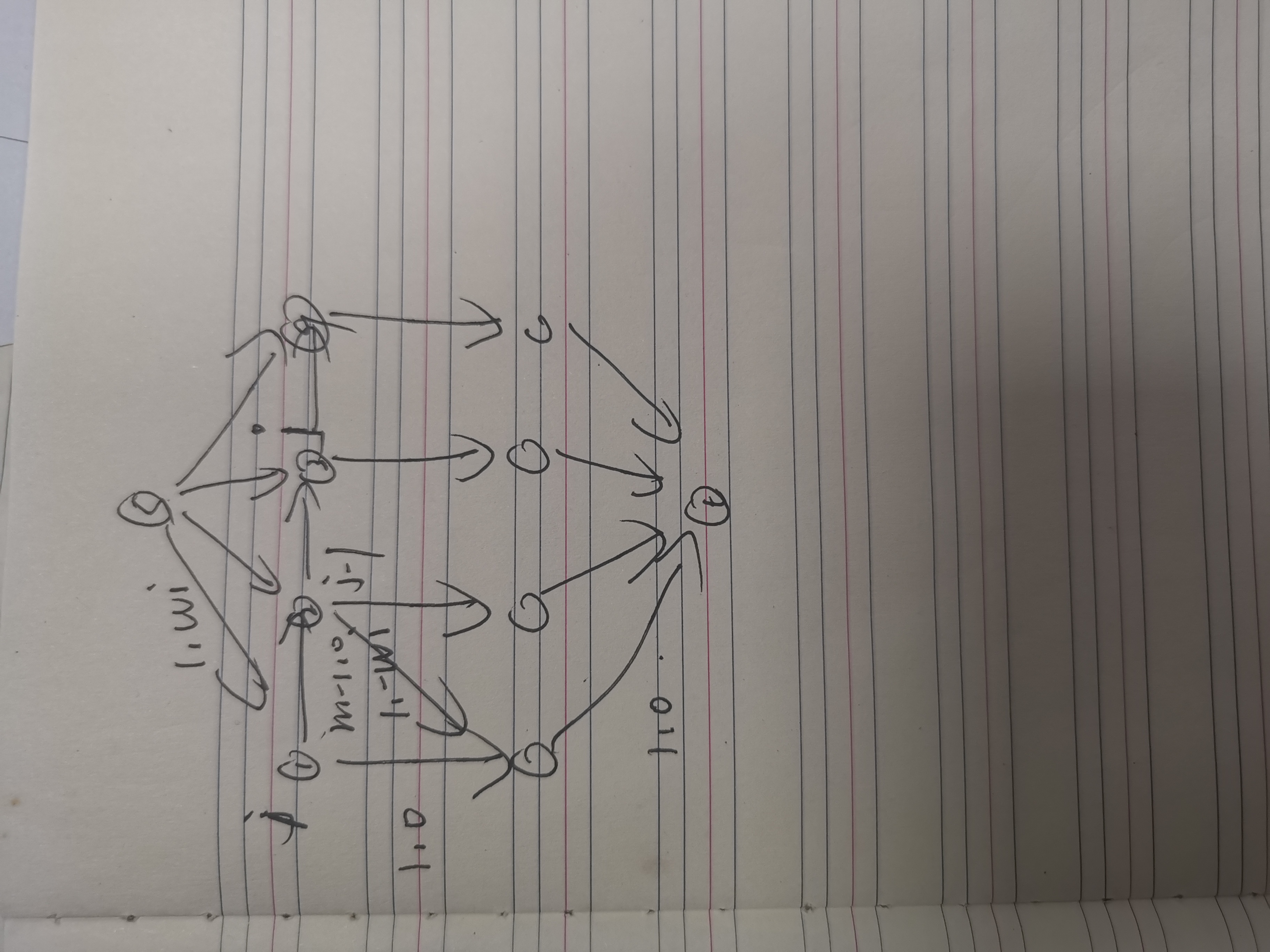
	for (i=0;i<=q;i++) ins(i,i+1,m-1,0);
	for (i=1;i<=q;i++) {
		ans+=w[a[i]];
		if (p[a[i]]) {
			int pre=p[a[i]];
			if (pre==i-1) ans-=w[a[i]];
			else ins(pre,i-1,1,-w[a[i]]);
		}	 
		p[a[i]]=i;
	}
	EK::EK(s,t);
	printf("%lld\n",ans+EK::anss);
	return 0;
}