NOIP模拟赛 10.29 by FXT and ZJ

, , ,

前言

被干爆了。

T1

Description

给定 $n$，求满足 $1\le x,y\le n,x^2-y=k^2,k\in N$ 的 $x,y$ 对数。

$n\le 10^{12}$。

Solution

移项有 $(x+k)(x-k)=y$，枚举 $x-k$ ，计算 $x+k$ 的数量。注意两者要奇偶相同。二分也可以，直接算也可以。我用了二分，减少（大脑）计算量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define maxn
#define put() putchar('\n')
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
using namespace std;
inline void read(int &x){
    int f=1;x=0;char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
    while (c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
    x*=f;
}
namespace Debug{
	Tp void _debug(char* f,Ty t){cerr<<f<<'='<<t<<endl;}
	Ts void _debug(char* f,Ty x,Ar... y){while(*f!=',') cerr<<*f++;cerr<<'='<<x<<",";_debug(f+1,y...);}
	Tp ostream& operator<<(ostream& os,vector<Ty>& V){os<<"[";for(auto& vv:V) os<<vv<<",";os<<"]";return os;}
	#define gdb(...) _debug((char*)#__VA_ARGS__,__VA_ARGS__)
}using namespace Debug;
const int mod=998244353;
int ans;
void add(int &x,int y) {x=(x+y)%mod;}
signed main(void){
//	freopen("1.in","r",stdin);
	int n;
	int i,j;
	read(n);
//	for (i=1;i<=n;i++) {
//		for (j=i;i*j<=n;j+=2) ans++;
//	}
	for (i=1;i*i<=n;i++) {
		int l=0,r=n/i+1;
		while (l+1<r) {
			int mid=l+r>>1;
			if ((mid*2+i)*i<=n) l=mid;
			else r=mid;
		}
		add(ans,l+1);
	}
	printf("%lld",ans);
	return 0;
}

T2

Description

https://qoj.ac/contest/1382/problem/7566

Solution

第一步差分没想到，题目做傻了，大家警戒。

区间加，考虑差分。目标是 $b_i$ 都变成 $0$。

观察到可以减少一次操作当且仅当 $\sum\limits_{i\in S} b_i=0$。直接 dp 就行。

可以枚举子集，但发现很多余。

根据差分。？枚新加的哪个数就可以了。在 $\sum b_i=0$ 的时候贡献 $+1$。

可能需要卡常。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#define lowbit(x) ((x)&(-(x)))
int f[(1<<23)+5],a[55],n;
ll s[(1<<23)+5],b[55];
void solve(void) {
	int i,j;
	read(n);
	for (i=1;i<=n;i++) read(a[i]);
	for (i=1;i<=n;i++) b[i]=a[i]-a[i-1],s[(1<<i-1)]=b[i];
	int N=(1<<n);
	for (i=1;i<N;i++) {
		f[i]=0;
		s[i]=s[i^lowbit(i)]+s[lowbit(i)];
		for (j=i;j;j-=lowbit(j)) f[i]=max(f[i],f[i^(lowbit(j))]);
		if (s[i]==0) f[i]++;
	}
	printf("%d\n",n-f[N-1]);
}
signed main(void){
	int T;
	read(T);
	while (T--) solve();
	return 0;
}

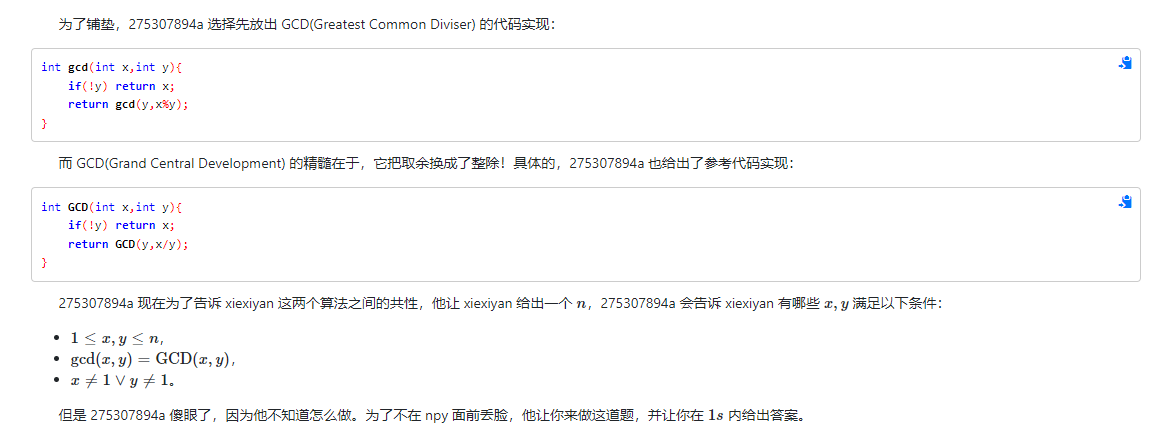
T3

Description

image-20231029162736654

$n,q \le 2\times 10^5$。

Solution

如果写过暴力的话，就发现满足条件的 $x,y$ 一定有 $x>y$ 且数量大约是 $O(n\log n)$ 级别的，想到做完所有答案最后输出。

观察到 $\text{GCD}(x,y)=\text{GCD}(y,\left\lfloor\dfrac{x}{y}\right\rfloor)$，考虑枚举 $y$ 和 $\left\lfloor\dfrac{x}{y}\right\rfloor=z$，$\text{GCD}$ 函数最多只有 $O(n\ln n)$ 种取值，对于每种 $y,z$ ，算出 $x$ 对应的范围，然后枚举 $\gcd$，暴力判断。实测跑的很快。

复杂度大约 $O(n\log ^2 n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define maxn
#define put() putchar('\n')
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
using namespace std;
void read(int &x){
    int f=1;x=0;char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
    while (c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
    x*=f;
}
namespace Debug{
	Tp void _debug(char* f,Ty t){cerr<<f<<'='<<t<<endl;}
	Ts void _debug(char* f,Ty x,Ar... y){while(*f!=',') cerr<<*f++;cerr<<'='<<x<<",";_debug(f+1,y...);}
	Tp ostream& operator<<(ostream& os,vector<Ty>& V){os<<"[";for(auto& vv:V) os<<vv<<",";os<<"]";return os;}
	#define gdb(...) _debug((char*)#__VA_ARGS__,__VA_ARGS__)
}using namespace Debug;
#define fi first
#define se second
#define mk make_pair
const int mod=1e9+7;
int power(int x,int y=mod-2) {
	int sum=1;
	while (y) {
		if (y&1) sum=sum*x%mod;
		x=x*x%mod;y>>=1;
	}
	return sum;
}
int gcd(int x,int y){
    if(!y) return x;
    return gcd(y,x%y);
}
int GCD(int x,int y){
    if(!y) return x;
    return GCD(y,x/y);
}
int n,q;
pair<int,int> ans[5000005];
int cnt;
signed main(void){
	int i,j,x,y,z;
	read(n);read(q);
	for (y=2;y<=n;y++) {
		for (z=1;z<=n/y;z++) {
			int xl=y*z,xr=min(n,y*(z+1)-1),tmp=GCD(y,z);
//			gdb(y,z,xl,xr,tmp);
			if (y%tmp) continue;
			for (i=(xl-1)/tmp*tmp+tmp;i<=xr;i+=tmp) if (gcd(i,y)==tmp) ans[++cnt]=mk(i,y);   
		}
	} 
	sort(ans+1,ans+1+cnt);
	while (q--) {
		read(x);
		if (x>cnt) puts("-1 -1");
		else printf("%d %d\n",ans[x].fi,ans[x].se);
	}
	return 0;
}

T4

数据分治题。算时间复杂度的时候感觉很妙啊，但是不太想写。