斜率优化学习笔记

, ,

斜率优化学习笔记

写在前面

很早以前写的了，看着当时写的很认真，所以发到自己的博客上去。

〇、前言

本来最近一段时间是想搞网络流的。结果最近几天老师要讲斜率优化，加上之前想学但是没看懂，就有了这篇学习笔记。

感谢 这篇博客 让我看懂了斜率优化。

一、基本概念

目前我所了解的，斜率优化是用来优化 $dp$，形如：
$$
f_i=\min / \max{f_j+A_i\times B_j+C_j+D_i}
$$
看起来与单调队列的：
$$
f_i=\min/\max{f_j+A_i+B_j}
$$
有点类似，因为斜率优化正是利用单调队列来实现的。

不过这不重要。重要的是理解思想。

二、算法介绍

首先看一道经典例题：

P3195 [HNOI2008]玩具装箱

设 $f_i$ 为以 $i$ 结尾的最小总费用。不难想到 $n^2$ 的 $dp$ 转移方程，如果想不到的话建议巩固 $dp$ 基础：
$$
f_i=\min\limits_{0\le j<i}{f_j+(sum_i+i-sum_j-j-L-1)^2}
$$
将与 $i$ 相关的放在一起，与 $j$ 相关和常数项的放在一起。事实上，常数项也可以和 $i$ 相关的放在一起。

令 $A=sum_i+i,B=sum_j+j+L+1$，则原式化简为：
$$
f_i=\min\limits_{0\le j<i}{f_j+(A-B)^2}=\min\limits_{0\le j<i}{f_j+A^2-2AB+B^2}
$$
为了方便，把 $\min$ 去了，然后把与只 $j$ 相关的项扔到等式右边，其他在左边：
$$
2A\times B+f_i-A^2=f_j+B^2
$$

$$
\begin{matrix}\underbrace{2A}\k\end{matrix}\times \begin{matrix}\underbrace{B}\x\end{matrix}+\begin{matrix}\underbrace{f_i-A^2}\b\end{matrix}=\begin{matrix}\underbrace{f_j+B^2}\y\end{matrix}
$$

问题转化成了：我们可以将经过许多点 $P_j(B_j,f_j+B_j^2)$ ，斜率为 $2A$ 的直线，所得的最小截距$(f_i-A^2)$的点为最佳转移点。

如何求这最佳转移点呢，还是要对于每次转移，$O(n)$ 的时间扫一遍吗？

我们先看一个问题，如下图，对于经过两个点 $N(a_1,b_1),M(a_2,b_2)$ ，$a_1<a_2$，斜率都为 $k$ 的直线，什么时候经过 $N$ 的截距小呢？什么时候经过 $M$ 点的截距小呢？

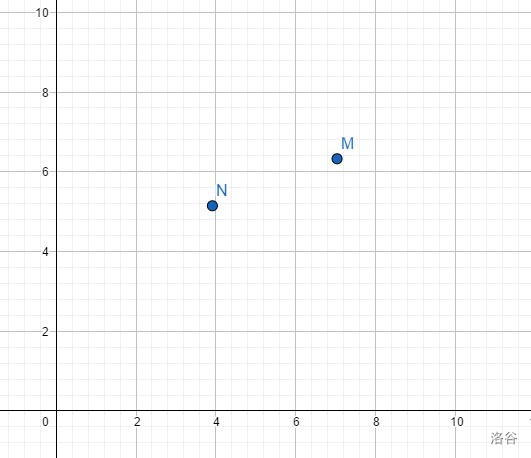
考虑先写出直线方程 ：

对于 $N$点 ，$y-b_1=k(x-a_1)$ ，化简得 截距$B_1=b_1-k\cdot a_1$

对于 $M$点，$y-b_2=k(x-a_2)$ ，化简得 截距$B_2=b_2-k\cdot a_2$

如果 $N$ 点截距小，则 $B_1<B_2$ 解得 $k<\dfrac{b_1-b_2}{a_1-a_2}$

如果 $M$ 点截距小，则 $B_1>B_2$ 解得 $k>\dfrac{b_1-b_2}{a_1-a_2}$

回到原题，我们发现 $A=sum_i+i$ 是单调递增的。也就是说，斜率 $k$ 随着转移点 $i$ 的增大而增大。

对于斜率 $k$ 不单调递增的情况下，我们后文会接着讨论。

对于两个点 $P_j(a_j,b_j)$ 和 $P_k(a_k,b_k)$ ，$a_j<a_k$ ，如果此时 $k<\dfrac{b_j-b_k}{a_j-a_k}$ ，那么转移 $j$ 点，反之转移 $k$ 点，而且之后再也不会转移到 $j$ 点。类似一个弹出操作。你可能会想到用一个数据结构维护这个弹出操作，是什么呢？

正是我们前文讲到的单调队列！

巧的是，每个转换而来的点 $P_j(B_j,f_j+B_j^2)$ ，其中 $B_j$ 也都是递增的，这表明着可以将点 $P_j$ 插入队尾而不需要插入中间的某一位置。

对于 $B_j$ 不单调递增的情况下，我们后文会接着讨论。而且现在我也没有遇到过。

现在，已经转移好了 $i$ 点，可是如何将 $i$ 点从队尾加入了这单调队列，转移其他的点呢？

如下图，假设我们现在又有三个点，分别是 $P_1(a_1,b_1),P_2(a_2,b_2)$ 和我们将要加入的点 $P_3(a_3,b_3)$，其中 $a_1<a_2<a_3$。

为了方便叙述，我们定义 $k_1=\dfrac{b_1-b_2}{a_1-a_2},k_2=\dfrac{b_2-b_3}{a_2-a_3},k_3=\dfrac{b_1-b_3}{a_1-a_3}$。

  1. 对于 $k_1<k_2$ 的情况


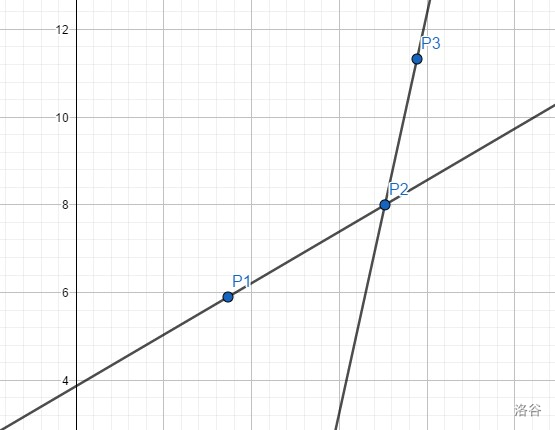
对于斜率 $k$：

  • 如果使 $P_1$ 截距最小，$k<k_1$

  • 如果使 $P_2$ 截距最小，$k_1\le k<k_2$

  • 如果使 $P_3$ 截距最小，$k2\le k$

  1. 对于 $k_1>k_2$ 的情况

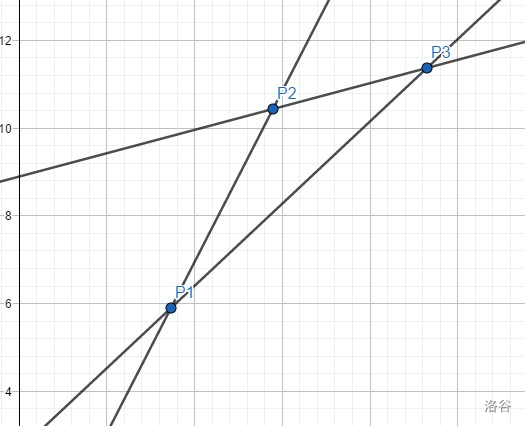
对于斜率 $k$：

  • 如果使 $P_1$ 截距最小，$k<k_3$

  • 如果使 $P_2$ 截距最小，无解，所以无论如何，最小截距也就是最优转移点，一定不是 $P_2$。

  • 如果使 $P_3$ 截距最小，$k3\le k$

所以，我们要在单调队列中维护斜率严格递增的一个点集，具体的，维护一个下凸包。这是取 $\min$ 的情况。相同的，取 $\max$ 就得维护一个上凸包。

回顾一下整个流程：

  1. 如果队列前两个点的斜率小于 $k$，则踢出队首。
  2. 取队首作为转移点。
  3. 将转移点 $i$ 入队之前，维护一个斜率递增的单调队列。如果下降，则弹出队尾。

代码就很简单了。

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
#define maxn 100005
#define rg register
#define int long long 
#define ll long long
#define put() putchar('\n')
using namespace std;
inline void read(int &x){
	int f=1;x=0;char c=getchar();
	while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
	while (c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
	x*=f;
}
int n,l,head,tail,q[maxn];
int sum[maxn],A[maxn],B[maxn],a[maxn],f[maxn];
inline double X(int i){return B[i];}
inline double Y(int i){return f[i]+B[i]*B[i];}
inline double slope(int i,int j){return (Y(i)-Y(j))/(X(i)-X(j));}
signed main(){
//	freopen("1.in","r",stdin);
    rg int i;
    read(n);read(l);
    for (i=1;i<=n;i++) read(a[i]),sum[i]=sum[i-1]+a[i];
    for (i=0;i<=n;i++) A[i]=sum[i]+i,B[i]=sum[i]+i+l+1;
    head=tail=1;
    for (i=1;i<=n;i++){
    	while (head<tail&&2*A[i]>=slope(q[head],q[head+1])) head++;
        //弹出队首
    	f[i]=f[q[head]]+A[i]*A[i]-2*A[i]*B[q[head]]+B[q[head]]*B[q[head]];
        //Update
    	while (head<tail&&slope(q[tail-1],q[tail])>=slope(q[tail],i)) tail--;
        //维护上凸包
    	q[++tail]=i;
	}
	printf("%lld",f[n]);
	return 0;
}

三、例题讲解

P2365 任务安排

虽然可以用 $O(n^2)$ 草过去，但是为了巩固斜率优化还是推荐大家再写一遍。

容易想到 $n^2 dp:$
$$
f_i=\min\limits_{0\le j<i}{f_j+s\times(sumC_n-sumC_j)+sumT_i\times(sumC_i-sumC_j)}
$$
看到有 $i$ 和 $j$ 的乘积，考虑斜率优化：

$$
f_i={f_j+s\times sumC_n-s\times sumC_j+sumT_i\times sumC_i-sumT_i\times sumC_j)}
$$
与 $j$ 有关的扔到右边：

$$
\begin{matrix}\underbrace{sumT_i+s}\k\end{matrix}\times \begin{matrix}\underbrace{sumC_j}\x\end{matrix}+\begin{matrix}\underbrace{f_i-sumT_i\times sumC_i}\b\end{matrix}=\begin{matrix}\underbrace{f_j+s\times sumC_n}\y\end{matrix}
$$
经过猜想+测试，以下整理也是可以的：

$$
\begin{matrix}\underbrace{sumT_i}\k\end{matrix}\times \begin{matrix}\underbrace{sumC_j}\x\end{matrix}+\begin{matrix}\underbrace{f_i-sumT_i\times sumC_i}\b\end{matrix}=\begin{matrix}\underbrace{f_j+s\times sumC_n-s\times sumC_j}\y\end{matrix}
$$
换言之，我们只需要把 $i,j$ 相关的相乘的项作为斜率 $k$ 。

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
#define maxn 100005
#define rg register
#define int long long 
#define ll long long
#define put() putchar('\n')
using namespace std;
inline void read(int &x){
	int f=1;x=0;char c=getchar();
	while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
	while (c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
	x*=f;
}
int n,head=1,tail=1,q[maxn];
int f[maxn],s,sumT[maxn],sumC[maxn],A[maxn],B[maxn];
inline double X(int i){return sumC[i];}
inline double Y(int i){return f[i]+s*(sumC[n]-sumC[i]);}
inline double slope(int i,int j){return (Y(i)-Y(j))/(X(i)-X(j));}//字面意思
signed main(){
	rg int i,x,y;
	read(n);read(s);
	for (i=1;i<=n;i++){
		read(x);read(y);
		sumT[i]=sumT[i-1]+x;
		sumC[i]=sumC[i-1]+y;
	}
    for (i=1;i<=n;i++){
    	while (head<tail&&sumT[i]+s>=slope(q[head],q[head+1])) head++;
        //将斜率<=k的弹出队列
    	f[i]=f[q[head]]+s*(sumC[n]-sumC[q[head]])+sumT[i]*sumC[i]-sumT[i]*sumC[q[head]];
        //Update
    	while (head<tail&&slope(q[tail-1],q[tail])>=slope(q[tail],i)) tail--;
        //维护上凸包
    	q[++tail]=i;
	}
	printf("%lld",f[n]);
	return 0;
}

咕咕咕