线性规划学习笔记

,

线性规划学习笔记

〇、前言

本文是我对线性规划的一个整理。

主要参考了 zzq的博客 ，2016年国家集训队的两篇论文。

一、定义

1. 标准型线性规划

最大化 ：

$$
\sum\limits_{i=1}^nc_ix_i
$$

$$
s.t. \sum\limits_{i=1}^n a_{j,i}x_i\le b_j,1\le j\le m
$$

$$
x_i\ge 0,1\le i\le n
$$

为了避免在求解过程中由于正负号带来的变换不等号问题，于是有了另一种表示方式——松弛型。

2. 松弛型线性规划

最大化

$$
\sum\limits_{i=1}^nc_ix_i
$$

$$
s.t. x_{i+n}=b_i-\sum\limits_{j=1}^n a_{i,j}x_j,1\le i\le m
$$

$$
x_j\ge 0,1\le j\le n+m
$$

二、求解——单纯形算法(Simplex algorithm)

求解范围：$b_i\ge0$

1. 定义

  • 在松弛型等式左侧的变量我们成为 基变量。

  • 在松弛型等式右侧的变量我们称为 非基变量。

线性规划中每一组限制都隐藏这一组基本解，对于 $x_{i+n}=b_i-\sum\limits_{j=1}^n a_{i,j}x_j,1\le i\le m$，有基本解 $x_{i+n}=b_i,x_j=0$。

2. 算法概述

单纯形算法有两个基本的操作 —— 转轴操作（Pivot） 和 **求解过程 (Simplex)**。

Pivot

转轴操作是对于一组限制中一个基变量 $x_A$ 和一个非基变量 $x_B$ 代换的操作。

我们称 $x_A$ 为换入变量，$x_B$ 为换出变量。

具体的说：

$$
x_{A}=b_i-\sum\limits_{j=1}^n a_{i,j}x_j
$$
把 $x_B$ 代换到等式左边，得：

$$
x_B=\dfrac{b_i-x_A-\sum\limits_{j=1,j\not = B}^na_{i,j}x_j}{a_{i,B}}
$$
当然在选择的时候要确保 $a_{i,B}\not= 0$。

用这条等式代替原等式，然后将这条等式依次带入其他等式和要优化的结果。

Simplex

Simplex 就是单纯形算法的主过程，从一个基本解出发，经过一系列的转轴操作，达到最优解。通过选择特定的换入变量和换出变量，使每一次转轴操作都能使目标函数增大，直到达到全局最优解。

基本过程：

  • 选择一个满足 $c_e \ge 0$ 的非基变量 $x_e$。
  • 找到那个满足 $a_{l,e} > 0$ 且 $\dfrac{b_l}{a_{l,e}}$ 最小的基变量 $x_{n+l}$。
  • 执行 $pivot(l,e)$ 然后回到第一步。

每次选择一个增大后可以使当前状态变优的变量，将其增加到有一个基变量变成 $0$ 位置，然后互换他们的位置。

第二步取最小的目的是一个贪心优化，可以使 $pivot$ 的次数降低许多。

该过程在一下两种情况下会终止：

  • 找不到一个合法的 $e$ ，显然现在已经找到了最优解。可以手模一组数据。
  • 找不到一个合法的 $l$ ，此时的最优解是 $\infty$ 。

可能还是有点懵，我们拿论文里的例子模拟一下。

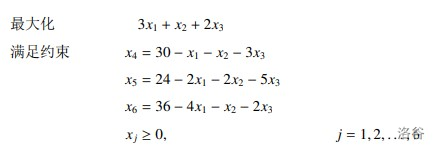
至于为什么是负号。如果看的仔细的话，前面线性规划的式子，每个 $a_{i,j}$ 之前都有个负号。

对于 $x_1$ ，显然在第三个限制 $\dfrac{b_3}{a_{3,1}}$ 最小。所以 $x_1$ 和 $x_6$ 互换位置，有了下边：

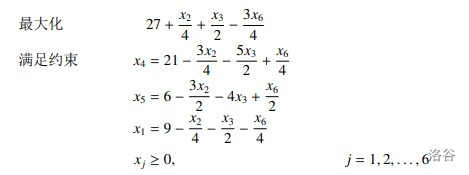
再对于 $x_3$ ，对于第 $2$ 条限制最小，$x_3$ 和 $x_5$ 互换位置。

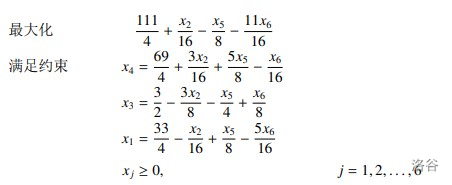
对于 $x_2$ 也是同理。

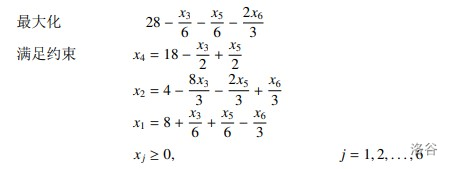
现在，由于 $c_i< 0,1\le i\le n，x_i\ge 0$ ，显然 $x_3=x_5=x_6=0$ 原式有最大值。最大值就是 $28$。基变量的值就是 $b_i$ 。此时的最优解就是 $x={8,4,0,18,0,0}$。

单纯形算法的核心思想就是这样，把 $c_i\le 0$ ，使得所有的非基变量都为 $0$ 。这就解释了为什么只能把 $b_i$ 全部搞成正的，负的反而会使答案边小。

3. 初始化过程

前文提到了 $Simplex$ 只能在 $b_i\ge 0$ 的时候进行。如果 $b_i<0$ 呢？这时候就要进行初始化。

具体的，初始化常见的有两种方法：新建一个辅助线性规划或者通过 $pivot$ 进行初始化。本文只介绍后一种方法。

根据 $pivot$ 的过程，在 $a_{i,B}>0$ 的情况下，$b_i$ 的正负性并不会被改变。所以当 $b_i$ 为负数时，只需要找到一个 $a_{i,j}<0$ 进行转轴操作即可改变 $b_i$ 的正负性。

当然，如果 $b_i<0$ 时，并没有找到 $a_{i,j}<0$ ，此时整个线性规划无解。

三、实现

代码细节比较多。

对于我这种写法，$a_{i,j},i>0,j>0$ 一定要取相反数！

其中 $id_i$ 是指取第 $i$ 条限制基变量的原序号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
const double eps=1e-8;
int id[maxn*2];
double a[maxn][maxn],vv[maxn];
int n,m,op;
inline int dcmp(double x){
	if (x>eps) return 1;
	else if (x<-eps) return -1;
	else return 0; 
}
namespace Semplex{
    inline void Pivot(int r,int c){
    	rg int i,j;double x=-a[r][c];
    	swap(id[n+r],id[c]);a[r][c]=-1;
		for (i=0;i<=n;i++) a[r][i]/=x;
    	for (i=0;i<=m;i++){
    		if (dcmp(a[i][c])&&i!=r){
    			x=a[i][c];a[i][c]=0;
    			for (j=0;j<=n;j++) a[i][j]+=x*a[r][j]; 
			}
		}
	}
	inline bool init(void){
		rg int x,y,i;
		for (i=1;i<=n;i++) id[i]=i;
		while (1){
			x=y=0;
			for (i=1;i<=m;i++) 
			    if (dcmp(a[i][0])<0&&(!x||rand()&1)) x=i;
			if (!x) return 1;
			for (i=1;i<=n;i++)
			    if (dcmp(a[x][i])>0&&(!y||rand()&1)) {y=i;break;}
			if (!y) {puts("Infeasible");return 0;}
			Pivot(x,y);
		}
    }
	inline void Semplex(void){
		rg int i,x,y,f;
		if (!init()) return;
		while (1){
			x=y=0;f=1;rg double w,t;
		    for (i=1;i<=n;i++) 
		        if (dcmp(a[0][i])>0&&(!x||rand()&1)) x=i;
		    if (!x) break;
		    for (i=1;i<=m;i++)
		        if (dcmp(a[i][x])<0&&(w=-a[i][0]/a[i][x],f||t>w)) y=i,f=0,t=w;
		    if (!y) {puts("Unbounded");return;}
		    Pivot(y,x);
		}
		printf("%.9lf\n",a[0][0]);
		if (!op) return;
		for (i=1;i<=n;i++) vv[i]=0;
		for (i=n+1;i<=n+m;i++) vv[id[i]]=a[i-n][0];
		for (i=1;i<=n;i++) printf("%.9lf ",vv[i]);
	}
} 
signed main(){
    rg int i,j;
    srand(time(0));
    read(n);read(m);read(op);
    for (i=1;i<=n;i++) scanf("%lf",&a[0][i]);
    for (i=1;i<=m;scanf("%lf",&a[i][0]),i++)
        for (j=1;j<=n;j++)
            scanf("%lf",&a[i][j]),a[i][j]*=-1;
    Semplex::Semplex();
	return 0;
}

四、对偶问题

给定一个原始线性规划：

最大化 ：

$$
\sum\limits_{i=1}^nc_ix_i
$$

$$
s.t. \sum\limits_{i=1}^n a_{j,i}x_i\le b_j,1\le j\le m
$$

$$
x_i\ge 0,1\le i\le n
$$

定义它的对偶线性规划为：

最小化：

$$
\sum\limits_{j=1}^mb_jy_j
$$

$$
s.t.\sum\limits_{j=1}^m a_{i,j}y_j\ge c_i,1\le i\le n
$$

$$
y_j\ge 0,1\le j\le m
$$

其最优解相同。

五、例题

[NOI2008] 志愿者招募

设 $M_{i,j}$ 表示第 $i$ 类志愿者在第 $j$ 天能否工作，$x_i$ 表示第 $i$ 类志愿者的数量。

易列出原始线性规划：

最小化

$$
\sum\limits_{i=1}^m x_ic_i
$$

$$
s.t.\ \sum\limits_{i=1}^m M_{j,i}x_i\ge a_j ,1\le j\le m
$$

$$
x_i\ge 0,1\le i\le m
$$

转化为其对偶线性规划：

最大化

$$
\sum\limits_{j=1}^n y_ja_j
$$

$$
s.t.\ \sum\limits_{j=1}^n M_{i,j}y_j\le c_i,1\le i\le m
$$

$$
y_j\ge 0,1\le j\le n
$$

$Code:$

1
2
3
4
5
6
7
8
9
10
11
12
signed main(){
    rg int i,j,l,r;
    srand(time(0));
    read(n);read(m);
    for (i=1;i<=n;i++) scanf("%lf",&a[0][i]);
    for (i=1;i<=m;i++){
    	read(l);read(r);scanf("%lf",&a[i][0]);
    	for (j=l;j<=r;j++) a[i][j]=-1.0;//一定要取负号！！！！！！
	}
    Semplex::Semplex();
	return 0;
}

[ZJOI2013]防守战线

板子

[SHOI2004]最小生成树

非常显然，树边不增，非树边不减。

考虑到非树边一定大于等于在最小生成树的路径上的边权，所以直接列约束条件。

注意到线性规划的一列只有两个非零值，非常浪费空间，所以用 $map$ 代替。

$$
d+\sum\limits_{i=1}^nc_ix_{id_i},id_i\in [1,n+m],c_i< 0
$$